Ao falar da programação linear, deve-se referenciar o livro clássico de George B. Dantzig intitulado Linear Programming and Extensions, 1963.
Além disso, sugerimos outro livro clássico de Alexander Schrijver intitulado Theory of Linear and Integer Programming, 1986 e, também, o artigo de Donald Goldfarb e Michael J. Todd intitulado Linear Programming, 1989.
Todos eles, de certa forma, contribuíram não só para a história da programação linear (PL), como também para o seu desenvolvimento e sua aplicabilidade em diversas áreas.
As técnicas para resolver problemas da PL passou por uma série de melhorias, ainda mais levando em conta o surgimento dos computadores e o seu enorme avanço ao longo do tempo.
O que é Programação Linear?
Programação Linear (PL) é uma importante área da matemática aplicada, computação, programação matemática, ou pesquisa operacional, responsável por tratar de problemas formados por um objetivo e um conjunto de restrições.
Ela é amplamente utilizada em diversas áreas, como economia, engenharia, logística, finanças, produção e gestão empresarial, para ajudar na tomada de decisões baseadas em dados.
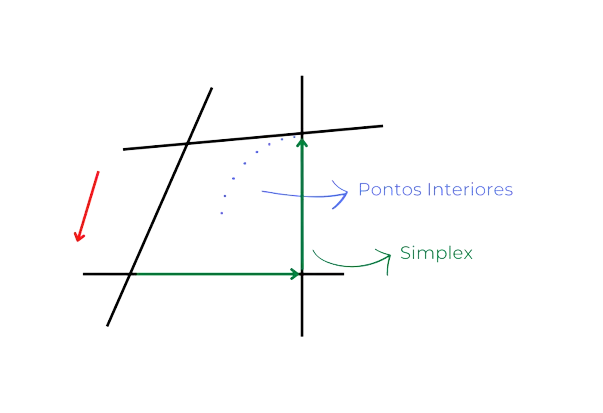
A solução ótima para um problema de PL é encontrada por meio de algoritmos de otimização, desenvolvidos especificamente para resolver estes problemas, como o método Simplex e os métodos de Pontos Interiores.
Qual é o objetivo da Programação Linear?
O objetivo da Programação Linear (PL) é encontrar a melhor solução possível para um problema de otimização linear sujeito a um conjunto de restrições.
Esse tipo de problema pode ser expresso matematicamente em termos de uma função linear (objetivo) a ser maximizada ou minimizada, sujeito a um conjunto de restrições lineares, que representam, por exemplo, as limitações de recursos do problema.
A solução ótima é encontrada quando a função objetivo é maximizada ou minimizada e todas as restrições são satisfeitas.
O objetivo da PL é, portanto, ajudar a tomar decisões sobre como, por exemplo, alocar recursos limitados de maneira eficiente e eficaz.
Ela pode ser usada para maximizar os lucros de uma empresa, minimizar os custos de produção, planejar o uso de recursos em um projeto, otimizar a alocação de mão de obra, maximizar o rendimento agrícola, entre outros.
Então, se trata de uma ferramenta poderosa para resolver problemas de otimização linear em uma ampla variedade de áreas, incluindo finanças, logística, engenharia, produção, gestão de projetos, marketing e muitas outras.
A utilização da PL ajuda a garantir que as decisões tomadas sejam baseadas em dados e em uma abordagem matemática sistemática, levando a resultados mais precisos e eficientes.
Quando começa a história da Programação Linear?
O famoso matemático, Fourier (1826), parece ter sido o primeiro a estudar desigualdades lineares de forma sistemática e de salientar a sua importância para a mecânica e teoria da probabilidade.
Ele estava interessado em encontrar o menor ajuste de desvio máximo (least maximum deviation fit) de um sistema de equações lineares, que ele reduziu ao problema de encontrar o ponto mínimo em um conjunto poliédrico.
Ele sugeriu uma solução de descida de vértice em vértice para um mínimo, que é o princípio por trás do método simplex usado hoje.
De que forma a Programação Linear se unificou?
Mais tarde, outro matemático famoso, de la Vallée Poussin (1911), considerou o mesmo problema e propôs uma solução similar.
No entanto, o matemático russo Leonid V. Kantorovich (1939) deve ser creditado como sendo o primeiro a reconhecer que certas classes importantes de problemas de produção tinham estruturas matemáticas bem definidas.
Ele ainda acreditava que elas eram passíveis de avaliação numérica prática e poderiam ser resolvidas numericamente.
Ainda, formulou e resolveu um problema de organização e planejamento de produção, cujo trabalho ficou desconhecido para o ocidente durante uns vinte anos.
Durante e imediatamente após a Segunda Guerra Mundial, trabalhos sobre esse tema e problemas similares tiveram procedimentos independentes até 1947.
Foi, então, em 1947 que a PL unificou os diversos temas fornecendo uma estrutura matemática e um método computacional, o algoritmo simplex
O intuito era o de formular tais problemas explicitamente e determinar as soluções deles eficientemente.
Esse desenvolvimento coincidiu com a construção de computadores eletrônicos digitais, os quais rapidamente se tornaram ferramentas necessárias na aplicação da Programação Linear.
Primeiros a financiar a Programação Linear
Durante a segunda guerra mundial, devido a escassez de recursos em diversos setores, os problemas enfrentados pelos militares era de enorme complexidade. Assim, o uso de técnicas matemáticas avançadas se fazia necessário.
Nesse período e imediatamente após o fim da guerra, a força aérea norte-americana financiou trabalhos em computadores eletrônicos e em técnicas matemáticas para resolver modelos de PL.
Trabalho intensivo iniciado em junho de 1947, em um grupo que mais tarde (outubro de 1948) foi dado o título oficial de Projeto SCOOP (Scientific Computation of Optimum Programs), implantado no Pentágono, com o objetivo de apoiar decisões de operações na força aérea norte-americana.
Foi aí que surgiu o método simplex, o qual foi desenvolvido, formalizado e testado, para resolver problemas de PL, pelo cientista norte-americano George B. Dantzig.
Dantzig publicou o algoritmo simplex no artigo científico intitulado “Maximization of a linear function of variables subject to linear inequalities“, em 1951.
Quando surgiu o termo “Programação Linear”?
Ao falar sobre a história da programação linear, acaba surgindo a dúvida e necessidade em saber quando surgiu esse termo.
O termo “programação linear” foi sugerido por Tjalling C. Koopmans, em 1951, como uma alternativa para o termo anterior, “programação em uma estrutura linear”.
O termo “programação” foi empregado porque os militares se referem ao planejamento de atividades como “programa” (program ou schedule).
O termo “formulação” (model building), refere-se ao processo de agrupar símbolos representando objetos de acordo com certas regras, para formar uma estrutura, o modelo, que corresponde a um sistema sob estudo no mundo real.
O boom da Programação Linear
Após o fim da segunda guerra mundial, a indústria logo observou que as técnicas de Programação Linear (PL), que haviam sido empregadas em problemas militares, poderiam também ser aplicadas em seus problemas e, assim, trazer enormes benefícios.
Minimizando custos e maximizando lucros, nos mais diversos setores, a PL passou a ser indispensável para a sobrevivência e o crescimento de companhias de grande e médio porte ao redor do mundo.
Assim, com esse grande interesse econômico, o desenvolvimento da PL seguiu a passos largos.
No meio acadêmico não foi diferente, o interesse pela PL foi enorme. A explosão da fama em torno da PL e do algoritmo simplex fez surgir várias perguntas teóricas relevantes.
Desde então, diversos matemáticos, e cientistas de outras áreas, foram atraídos e passaram a dedicar suas pesquisas nestes temas.
Onde se aplica a Programação Linear?
A programação linear pode ser vista, então, como uma técnica matemática usada para otimizar problemas de alocação de recursos sujeitos a certas restrições. Ela pode ser aplicada em diversas áreas, incluindo:
- Produção: na área de produção, a programação linear é uma técnica matemática amplamente utilizada para otimizar a alocação de recursos e minimizar custos, maximizando os lucros.
- Logística: na logística, a programação linear é uma ferramenta importante para otimizar a alocação de recursos em sistemas de transporte, como rotas de transporte, distribuição de mercadorias e alocação de frota.
- Finanças: em finanças, a programação linear é útil para otimizar a alocação de investimentos em carteiras de ações e outros instrumentos financeiros, maximizando o retorno e minimizando os riscos.
- Energia: a programação linear é usada para otimizar a alocação de recursos em sistemas de geração e distribuição de energia, incluindo o planejamento de redes elétricas e a gestão de usinas hidrelétricas.
- Marketing: a programação linear pode ser utilizada para otimizar campanhas publicitárias, incluindo a alocação de recursos em diferentes canais de mídia e o planejamento de orçamentos de publicidade, maximizando o retorno sobre o investimento.
Desenvolvimento da Programação Linear no meio acadêmico
Em teoria da computação, um algoritmo é considerado eficiente quando o seu número de passos for limitado polinomialmente.
Em 1972, Klee e Minty construíram um exemplo para estabelecer a não polinomialidade do algoritmo simplex para um certo critério de escolha para a entrada na base.
A partir daí, vários outros exemplos inviabilizaram novos critérios de escolha. Algoritmos do tipo elipsóide foram introduzidos para programação convexa.
Em 1979, Khachiyan utilizou o método dos elipsóides para o problema de viabilidade de PL com dados inteiros.
Khachiyan definiu o número L e mostrou que seu algoritmo resolve o problema de PL em tempo polinomial.
Em 1984, Karmarkar publicou seu algoritmo de pontos interiores baixando a complexidade em relação ao método de Khachiyan.
Atualmente, a menor complexidade é O((n3/ln(n))L) obtida por Anstreicher em 1999.
Bixby, Gregory, Lustig, Marsten e Shanno (1992) resolveram um problema de PL, os quais tratam com um algoritmo híbrido ponto interior/simplex, específico para um problema que aparece no planejamento de tripulação aérea.
Em 2006, Gondzio e Grothey resolveram um problema com 1 bilhão de variáveis usando pontos interiores.
Embora na teoria o método simplex possua complexidade exponencial, enquanto os métodos de pontos interiores são de complexidade polinomial, ele ainda é bastante utilizado, pois na prática ele se mostra muito eficiente na resolução de problemas de tamanho moderado.
Conclusão
Portanto, como vimos no texto, a programação linear é uma importante área de estudos voltada para o desenvolvimento e aplicação de técnicas matemáticas e computacionais, capazes de resolver problemas dos mais variados setores.
Do ponto de vista teórico, as famílias dos métodos simplex (algoritmo simplex primal, algoritmo simplex dual e algoritmo simplex primal-dual), pontos interiores e ponto interior inviável, consistem na mais relevante contribuição para a linha de algoritmos de otimização.
Além de todos estes algoritmo citados acima serem exatos, isto é, se pode provar matematicamente que a solução gerado por eles é ótima para o problema, os métodos de pontos interiores possuem complexidade polinomial, o que é extremamente importante para se conseguir escalabilidade.

Pelas contribuições para a teoria de locação ótima de recursos, Koopmans e Kantorovich foram condecorados com o Prêmio Nobel em Economia (1975).
As contribuições de Dantzig para a Otimização, dentre elas a criação do método Simplex, são tantas que em 1979 as renomadas sociedades científicas internacionais SIAM (Sociedade de Matemática Aplicada e Industrial) e MOS (Sociedade de Otimização Matemática) estabeleceram o importante Prêmio George B. Dantzig.
Perguntas frequentes sobre programação linear (FAQs)
No que se refere à perguntas básicas sobre programação linear, podemos mencionar as seguintes:
O que é Programação Linear?
Programação Linear é uma técnica de otimização matemática que busca maximizar ou minimizar uma função linear sujeito a um conjunto de restrições lineares.
Qual é a diferença entre Programação Linear e Programação Não Linear?
Programação Linear é limitada a problemas em que a função objetivo e as restrições são lineares. Já a Programação Não Linear permite que a função objetivo e/ou as restrições sejam não lineares.
Como resolver um problema de Programação Linear?
Um problema de Programação Linear pode ser resolvido usando métodos como os da família Simplex, ou métodos de Pontos Interiores. Enquanto os métodos Simplex procuram a solução ótima movendo-se ao longo das fronteiras do conjunto viável, os de Pontos Interiores trabalham com pontos em que suas coordenadas são todas não nulas.
O que é Programação Inteira?
A Programação Inteira é uma extensão da Programação Linear em que as variáveis de decisão são restritas a serem números inteiros. Isso significa que as soluções possíveis são limitadas a valores inteiros, em vez de valores fracionários.

