Matrizes, conceitos, exemplos, aplicações e tipos especiais

As matrizes são ferramentas fundamentais e amplamente estudadas em diversas áreas, tais como matemática, ciência da computação, física, nas engenharias e muitas outras áreas.

Elas nos permite representar e manipular dados em forma de tabelas, o que as tornam úteis em muitos problemas das áreas citadas acima.

Neste artigo, e nos seguintes com as operações matriciais, vamos discutir o que são, seus tipos, definições, algumas aplicações e como realizar operações com matrizes, como multiplicação, transposição, inversão e resolução de sistemas de equações lineares. 

Entenderemos a sua importância em várias áreas e como elas podem ser usadas para resolver problemas complexos. 

Acompanhe-nos nesta jornada para descobrir as maravilhas das matrizes e como elas estão presentes em muitos aspectos do nosso dia a dia.

Conceitos básicos

Dentre os conceitos básicos sobre matrizes, podemos citar:

O que são? 

Em suma, são estruturas de dados, normalmente compostas por números, com uma ou mais dimensões. Quando elas possuem apenas uma dimensão, são conhecidas como vetores.

Dimensões

Excluindo os vetores, as matrizes são predominantemente de duas dimensões, ou seja, bidimensionais.

Neste caso, a primeira dimensão indica o número de linhas e a segunda dimensão indica o número de colunas.

Essa estrutura bidimensional é o que permite, por exemplo, a representação e manipulação de dados em forma de tabelas.

As matrizes bidimensionais também são usadas para representar sistemas lineares, para armazenar imagens, para representar transformações geométricas, entre muitas outras aplicações.

Além disso, existem também matrizes de três ou mais dimensões, que são usadas em aplicações como ciência de dados, inteligência artificial, entre outras.

Bidimensional vs 2×2

É importante não confundir matriz bidimensional com matriz 2×2, ou matriz de ordem 2. Esta última é apenas um caso particular de matriz bidimensional, formada por 2 linhas e 2 colunas.

Um exemplo prático

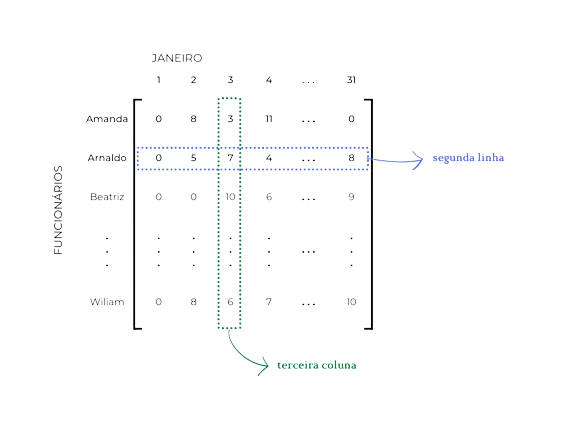
Para controlar as horas trabalhadas, em cada dia do mês de janeiro, de cada um de seus 50 funcionários, uma empresa pode utilizar uma matriz. 

Logo, tais informações podem estar em uma matriz bidimensional, com 50 linhas, uma para cada funcionário, e  31 colunas, uma para cada dia de janeiro. 

Definição

Portanto, dados dois números inteiros m e n, maiores do que 1, uma matriz bidimensional A, composta por m linhas e n colunas, pode ser representada como na figura abaixo. A notação A_m×n também é bastante usada, visando indicar as dimensões da matriz.

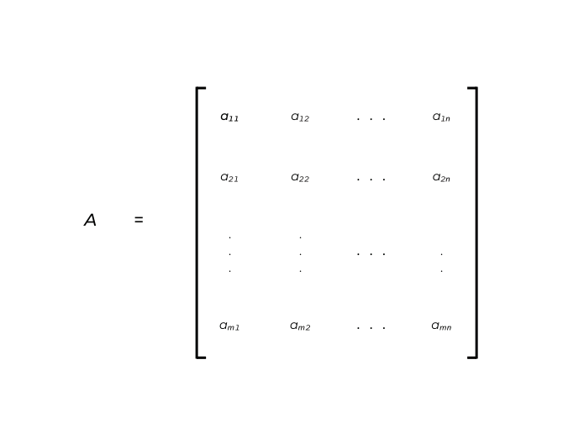
Neste caso, cada linha da matriz A possui n elementos. De modo análogo, também podemos dizer que cada coluna da matriz A possui m elementos.

Observe que cada linha de A pode ser vista como um vetor, pois possui apenas uma dimensão. Da mesma forma, cada coluna da matriz A também é um vetor.

Um elemento de uma matriz é identificado por sua posição nela, sendo representado por sua linha e sua coluna. Por exemplo, o elemento a₂₃ é aquele que se encontra na linha 2 e coluna 3 da matriz A.

Na matriz do exemplo prático, este elemento é o número 7. Isto significa que o funcionário Arnaldo (associada a linha 2) trabalhou 7 horas no dia 3 de janeiro (terceira coluna da matriz).

Tipos especiais de matrizes

Certas matrizes recebem um destaque especial, seja por estarem presentes em aplicações ou pelas suas relevâncias na fundamentação matemática e, também, em algoritmos para a resolução de problemas.

Matriz nula

As matrizes nulas são aquelas em que todos os elementos são iguais a 0 (zero). Em operações matriciais, as matrizes nulas atuam de modo similar ao número zero em operações com número reais.

Vejamos um exemplo na figura abaixo. Se trata da matriz nula, que vamos chamar de O, com duas linhas e três colunas.

Igualdade de matrizes

O primeiro requisito para que duas matrizes sejam iguais é a dimensão. Isto é, para que duas matrizes bidimensionais A e B sejam ditas iguais, o número de linhas delas devem ser o mesmo, assim como o número de colunas.

Além disso, é necessário que os elementos em posições correspondentes sejam iguais. Ou seja, a_ij deve ser igual a b_ij para qualquer linha i e coluna j das duas matrizes.

Matriz transposta

Para toda matriz, bidimensional, existe uma outra matriz associada a ela, chamada de matriz transposta.

Sendo A uma matriz com m linhas e n colunas, então a transposta de A é uma matriz com n linhas e m colunas.

Veja um exemplo na figura abaixo. Estamos chamando de B a matriz transposta de A.

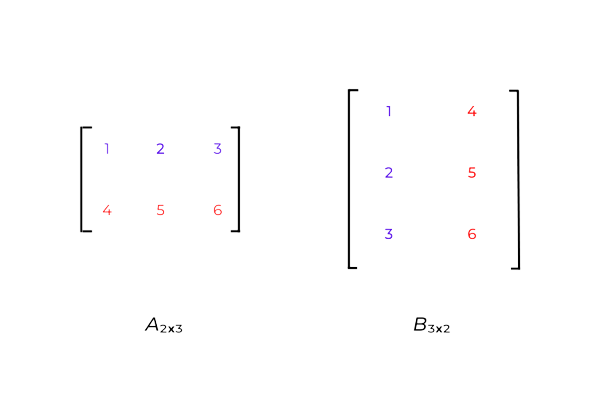
Note que as linhas de A são as colunas de B, e que as linhas de B formam as colunas de A.

De modo geral, a i-ésima linha de uma matriz é a i-ésima coluna da sua transposta.

Então, não deixe de observar que a transposta da transposta é a própria matriz. Isto é, a transposta da matriz B é a matriz A.

Observe, também, que elas possuem dimensões opostas. Ou seja, se uma matriz é mxn, sua transposta é nxm.

Em livros de matemática é comum você encontrar Aᵀ representando a transposta de A, ou Mᵀ para representar a transposta de uma matriz M. Isto são apenas detalhes de notação.

Matriz quadrada

São as matrizes em que o número de linhas e colunas é o mesmo.

Então pode se tratar de uma matriz 2×2, 3×3, 4×4, e assim por diante.

Muitas delas são bastante conhecidas e fundamentais no universo das matrizes. Por exemplo, a matriz identidade, as matrizes triangulares, a matriz inversa, dentre outras.

Estas matrizes serão apresentadas em tópicos abaixo. Acompanhe.

Matriz diagonal 

Antes de definir este tipo de matriz, precisamos saber o que é a diagonal de uma matriz. Este termo se aplica a matrizes quadradas.

Considerando D uma matriz quadrada nxn, sua diagonal (ou diagonal principal) é formada pelos elementos d₁₁, d₂₂, …, d_nn.

Dado isso, podemos definir a matriz diagonal. Isto é, se trata de matrizes quadradas em que todos os elementos fora da diagonal são nulos.

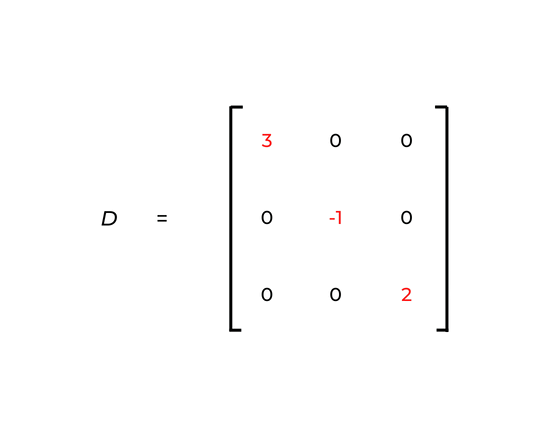
Por exemplo, qualquer matriz nula que seja quadrada também é uma matriz diagonal. Ou seja, é permitido ter o número zero também na diagonal principal.

Vejamos outros casos a seguir.

Matriz identidade

Matriz identidade é uma matriz quadrada que possui todos os elementos da diagonal principal iguais a 1 e todos os outros elementos da matriz iguais a 0.

Ela é similar ao número 1 nas operações de multiplicação de números reais.

Isto é, quando é possível multiplicar uma matriz A pela matriz identidade, o resultado é a própria matriz A.

Veja a operação de multiplicação de matrizes para observar este e outros fatos em torno deste tipo de matrizes.

Matriz triangular

As matrizes triangulares também são matrizes quadradas e podem ser separadas em dois grupos.

O das matrizes triangulares inferiores, que são aquelas em que todos os elementos acima da diagonal principal são iguais a zero.

E o das matrizes triangulares superiores, que são aquelas em que todos os elementos abaixo da diagonal principal são iguais a zero.

Na figura abaixo temos uma matriz triangular inferior L, 3×3, e uma matriz triangular superior U, 2×2.

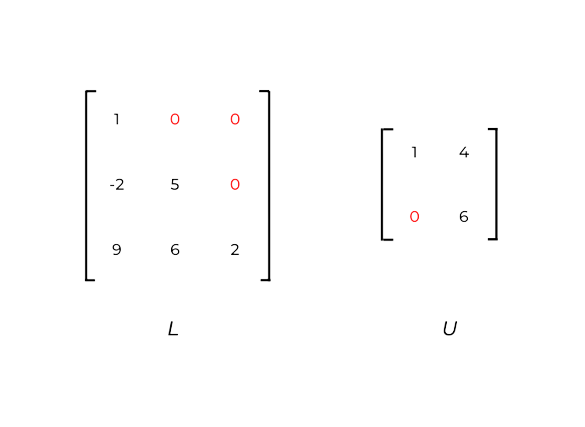
Matriz simétrica

Outro tipo especial de matriz quadrada são as matrizes simétricas. Nelas, a diagonal é vista como um espelho.

Em uma matriz simétrica, os elementos em posições opostas são sempre iguais. Isto é, o valor contido em uma linha i e coluna j da matriz é igual ao valor contido na linha j e coluna i.

Veja um exemplo na imagem abaixo.

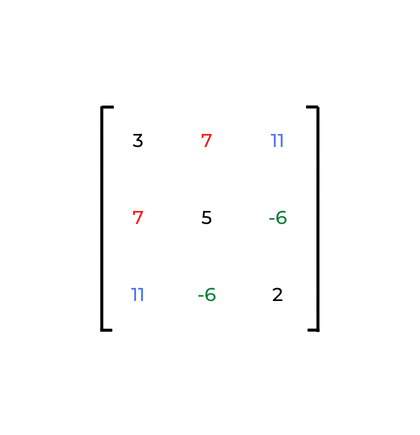
Temos, então, que as matrizes diagonal e a matriz identidade são matrizes simétricas.

Observe, também, que a matriz transposta de uma matriz simétrica é sempre ela mesma.

Agora que sabemos o que são matrizes, podemos descobrir o universo de suas operações e entender sua grande importância na resolução de problemas.

Então, continue essa jornada no material exclusivo que preparamos sobre Operações com Matrizes.

FAQs

Referências

https://portaldaobmep.impa.br/index.php/modulo/ver?modulo=75#