A resolução de sistemas de equações lineares é um tópico bastante difundido e fundamental, pois nas mais diversas áreas do conhecimento temos problemas que podem ser modelados e resolvidos com estas técnicas.
Então, venha conosco descobrir um pouco mais sobre os sistemas de equações lineares!
Um probleminha bancário
Antes de definições mais formais, vejamos um problema que pode ocorrer no nosso dia a dia, o qual podemos representar e resolver através de sistemas de equações lineares.
Suponha que você vá até o banco e retire de sua conta 130 reais, recebendo 9 notas, algumas de 10 reais e outras de 20 reais. Quantas notas de 10 reais você recebeu?
Para este problema, temos que definir duas variáveis, uma para representar a quantidade de notas de 10 reais e outra para representar a quantidade de notas de 20 reais, as quais vamos chamar de x1 e x2, respectivamente.
Agora, observe na descrição do problema que a soma de x1 com x2 deve ser igual a 9, que é o total de notas recebidas. Sua representação matemática é: x1 + x2 = 9.
Observe, também, que 10 vezes x1 mais 20 vezes x2 será o valor total retirado, isto é, 130 reais. Sua representação matemática é: 10x1 + 20x2 = 130.
Então, o problema consiste em encontrar os valores para x1 e x2 que atendem, simultaneamente, as duas equações. Sua representação é dada pelo sistema de equações lineares abaixo, figura (a).
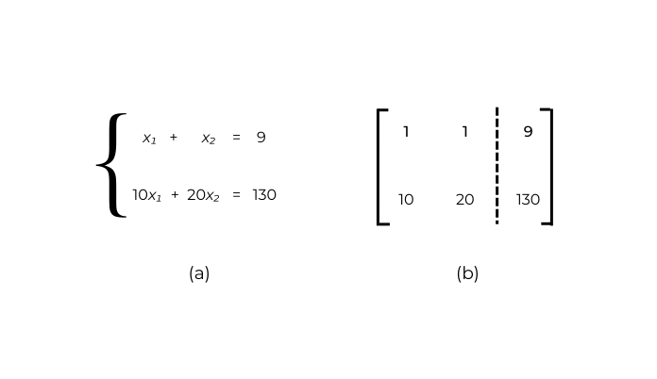
Dizemos que este sistema é dois por dois, 2×2, por conter exatamente duas variáveis e duas equações lineares.
Atenção estudantes do ensino médio, ou fundamental, questões desta natureza caem com frequência em provas de vestibulares e no ENEM.
Então, venha conosco e se prepare.
Bom, a grande maioria dos problemas que surgem na prática, envolvendo sistemas de equações lineares, possuem muito mais variáveis e equações.
Deste modo, é importante sabermos técnicas para resolver sistemas 2×2, 3×3, ou de qualquer outra dimensão. A mais usual, e simples, é através do escalonamento da matriz aumentada do sistema.
No caso do exemplo anterior, a matriz aumentada do sistema está representada na figura (b), acima.
Observe que a matriz aumentada é formada pelos coeficientes associados as variáveis e pelos termos independentes do lado direito, separados pela barra tracejada.
De forma resumida, o escalonamento de matrizes é uma sequência de aplicações de operações elementares, descritas abaixo.
Operações elementares por linhas
Existem três tipos de operações que podemos aplicar nas linhas de uma matriz aumentada sem que a solução do problema seja alterada.
Elas visam simplificar a matriz de modo que uma solução para o problema seja facilmente obtida.
As três operações elementares são:
- Trocar duas linhas de posição;
- Multiplicar todos os elementos de uma linha por um número diferente de zero; e,
- Substituir uma linha pela soma (ou subtração) dela com outra linha multiplicada por um número.
Vamos aos exemplos. Considerando a matriz aumentada do sistema das notas de 10 e 20 reais, veja como seria aplicar cada uma das três operações.
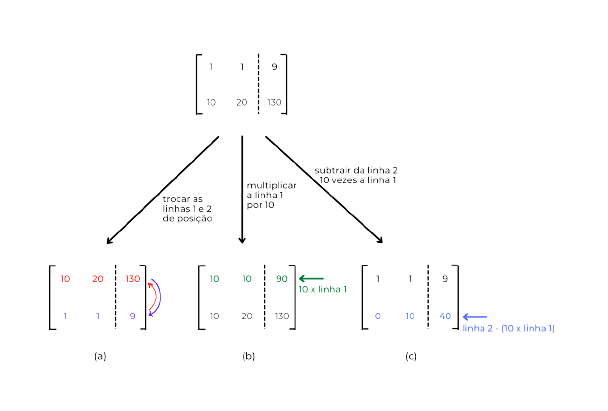
Na figura (a), temos uma operação de troca de linhas. Em (b), a multiplicação da primeira linha pelo número 10. Na figura (c) subtraímos, da linha 2, a linha 1 multiplicada por 10.
Observe que, para cada operação que desejamos aplicar, as contas devem ser feitas em todos os elementos da linha.
Veja, também, que com apenas a operação da figura (c) podemos obter a resposta para o probleminha das notas.
Após a operação temos, pela segunda linha, que 0x₁ + 10x₂ = 40, isto significa que o valor para x₂ é 4. E, como x₁ + x₂ = 9, então x₁ = 5.
Ou seja, foram retiradas 5 notas de 10 reais. Esta é a resposta para este pequeno problema.
E como seria se a gente quisesse obter a solução de forma mais direta? Vamos lá.
Processo de escalonamento
Para deixar a solução do nosso probleminha ainda mais clara, podemos continuar aplicando operações a partir da matriz aumentada representada na última figura (c).
Veja como seria o processo do início ao fim.
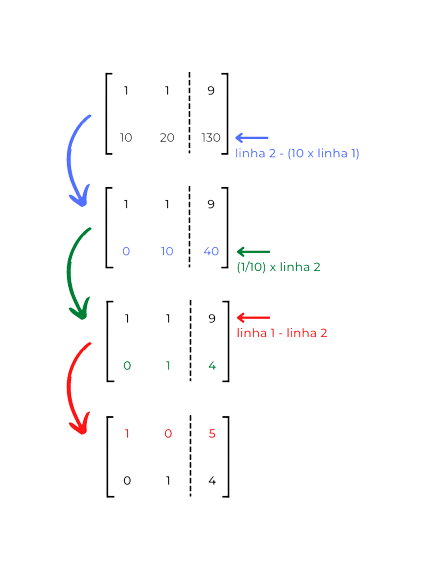
Esta última matriz aumentada nos diz que 1x₁ + 0x₂ = 5 e 0x₁ + 1x₂ = 4. Ou seja, x₁ = 5 e x₂ = 4.
A sequência de operações realizadas acima, nada mais é do que a aplicação do clássico algoritmo de Gauss-Jordan, capaz de resolver sistemas de qualquer dimensão.
Portanto, para resolver um sistema de equações lineares, podemos aplicar operações elementares até ser possível descobrir os valores das variáveis, como fizemos através da matriz na figura (c), das operações elementares por linhas, ou até simplificar ao máximo o sistema, como feito neste último caso, escalonamento completo.
Através dos exemplos e exercícios práticos, ao final deste artigo, iremos compreender melhor qual operação aplicar, em cada situação, ao longo do processo de escalonamento.
Sempre com a finalidade de obter um sistema equivalente pelo qual uma solução para o problema seja clara.
Outro ponto fundamental que precisamos saber, antes de irmos para a prática, diz respeito a como os sistemas de equações lineares podem ser classificados.
Classificação dos sistemas
Existem três possibilidades para os sistemas de equações lineares. Ele pode possuir uma única solução, possuir uma infinidade de soluções ou não admitir nenhuma solução.
Sistema possível e determinado
Todos os sistemas de equações lineares que possuem uma única solução é classificado como possível e determinado.
Por exemplo, o sistema do probleminha bancário. Como vimos, a solução para ele é definida por x₁ = 5 e x₂ = 4.
Temos que ela é única, dada a sua clara identificação após o processo de escalonamento, realizado na seção anterior.
Sistema possível e indeterminado
Agora, quando os sistemas de equações lineares possuem mais de uma solução, neste caso significa que ele possui uma infinidade de soluções, ele é dito possível e indeterminado.
Por exemplo, o sistema contendo apenas a equação x₁ + x₂ = 0. Temos que qualquer valor para x₂, de modo que x₁ seja igual a –x₂, indicará uma solução para o problema. Veja que (0, 0), (1, -1) e (-5, 5) são algumas das possíveis soluções.
Sistema impossível
Os sistemas de equações lineares para o qual não existe uma combinação de valores para as variáveis que atenda todas as igualdades é classificado como impossível.
Por exemplo, o sistema de equações lineares composto por x₁ + x₂ = 1 e x₁ + x₂ = 2. Veja que não existem números reais que x₁ e x₂ possam assumir de modo que as duas equações sejam atendidas ao mesmo tempo.
Bom, vamos para a prática com mais exemplos, passo a passo, e exercícios em que você toma as decisões.
Atividade sistemas de equações lineares
Antes de ir para a atividade, assista o vídeo explicativo abaixo. Nele você acompanha a resolução de um exemplo passo-a-passo através do processo de escalomamento de Gauss.
A atividade que preparamos para este tópico utiliza os apps A+Exemplo e A+Prática. Ela está disponível na versão anterior da APlus Platform e o link para a atividade se encontra no final desta página, em referências.
Conclusão
Neste texto fizemos uma introdução sucinta aos sistemas de equações lineares. Através de uma pequena aplicação dada, é possível se ter uma ideia da sua vasta aplicabilidade no mundo real. Também vimos como podemos usar técnicas para resolver estes problemas. Dentre elas, a matriz aumentada do sistema e as operações elementares por linhas são fundamentais para métodos como o de Gauss.
A atividade que preparamos na versão anterior da APlus Platform, disponiível no link abaixo, te permite avançar no estudo da resolução de sistemas de equações lineares. Com bastante prática e aplicativos exclusivos, esta atividade te possibilita se preparar para tópicos mais avançados de Álgebra Linear e Pesquisa Operacional, por exemplo. Aproveite a oportunidade e bons estudos!
Referências
Atividade sistemas de equaões lineares com os aplicativos A+Exemplo e A+Prática
Sistema de equações lineares – Wikipédia
Perguntas frequentes sobre sistemas de equações lineares
Como se resolve sistema de equações lineares?
Existem vários métodos para resolver sistemas de equações lineares, mas um dos mais comuns é o método da eliminação de Gauss-Jordan.
O objetivo deste método é transformar o sistema original em um sistema equivalente cujas equações sejam mais simples e fáceis de resolver.
Quais são os sistemas lineares?
Ao todo, existem três classificações para um sistema linear, que são os seguintes:
Sistema possível e determinado: que são aqueles que possuem uma solução única.
Sistema possível e indeterminado: onde há uma infinidade de soluções.
Sistema impossível: quando não existe solução.